La  nature aime les spirales logarithmiques : des tournesols aux coquillages, des tourbillons aux ouragans en passant par les immenses spirales galactiques, il semble que la nature ait choisi cette figure harmonieuse comme son ornement préféré. » (Mario Livio, astrophysicien israélien).
nature aime les spirales logarithmiques : des tournesols aux coquillages, des tourbillons aux ouragans en passant par les immenses spirales galactiques, il semble que la nature ait choisi cette figure harmonieuse comme son ornement préféré. » (Mario Livio, astrophysicien israélien).
La spirale logarithmique a été étudiée pour la première fois en 1638 par René Descartes (1596 - 1650), mais c'est le mathématicien suisse Jakob Bernoulli (1654 - 1705) qui a appelé cette courbe "Spira mirabilis", la spirale merveilleuse, et a demandé qu'elle soit gravée sur sa tombe à côté de la phrase "Eadem mutata resurgo", ou "bien que différente, je renais également".
Cette phrase latine contient le secret de cette spirale, et la raison pour laquelle elle est si présente dans la nature. Pour mieux comprendre ce secret, comme pour tout objet mathématique, il faut d'abord donner sa définition.
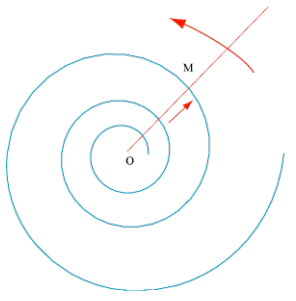
La spirale logarithmique est la trajectoire d'un point qui se déplace avec un mouvement uniformément accéléré sur une demi-droite qui tourne uniformément autour de son origine.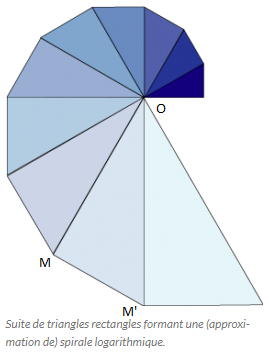
D'après la définition, nous pouvons facilement décrire l'abscisse et l'ordonnée du point mobile avec des équations trigonométriques et démontrer que la courbe obtenue est proportionnelle, c'est-à-dire que si nous considérons une succession discrète de points de la courbe, obtenue par une variation constante de l'angle de rotation, chaque segment [OM] sera plus long que le précédent selon un rapport constant, de sorte que la courbe ne change pas de forme en grandissant. En particulier, les distances entre les bras de la spirale augmentent selon une progression géométrique. C'est l'origine de la phrase choisie par Bernoulli pour son épitaphe.
Voyons maintenant pourquoi cette caractéristique de la spirale en fait le modèle le plus répandu en biologie.
Considérons le cas de la croissance du nautile. Le nautile est un mollusque marin dont la coquille est en forme de spirale. L’espace entre les spires étant triplé à chaque enroulement, elle évoque une spirale logarithmique. Pour examiner si cette forme est fortuite ou non, il est nécessaire d’en comprendre la provenance. La coquille du nautile est divisée en chambres closes, l’animal n’occupant que la dernière. Les autres sont remplies d’un mélange de liquide et de gaz, toutes communiquent entre elles au moyen d’un siphon. Ces chambres correspondent à l’évolution progressive du mollusque. Quand il grossit, ne pouvant agrandir la chambre où il se trouve, il en crée une autre dans son prolongement, un peu plus grosse mais semblable. On retrouve ainsi la propriété de proportionnalité, il s'agit alors d'une spirale logarithmique !

Et ce n'est qu'un exemple parmi beaucoup d'autres. Nous retrouvons la même spirale dans la structure des galaxies, ainsi que dans le chou romain que nous achetons au marché ou dans la disposition des feuilles de certaines plantes succulentes.



La phyllotaxie, ou l'étude de la disposition des différents éléments dans les plantes, explique que la croissance des branches, des feuilles, des graines et des écailles se fait de manière optimale et avec le moins de gaspillage possible : le but est de réduire le gaspillage d'espace.
 En 1907, G. van Iterson a démontré qu'une série de points, disposés selon l'angle de croissance (environ 137 degrés, le nombre d'or de l'angle de révolution), est perçue visuellement comme un couple de familles de spirales (spirales végétatives), l'une dans le sens des aiguilles d'une montre et l'autre dans le sens inverse, en quantités égales à deux nombres de Fibonacci consécutifs.
En 1907, G. van Iterson a démontré qu'une série de points, disposés selon l'angle de croissance (environ 137 degrés, le nombre d'or de l'angle de révolution), est perçue visuellement comme un couple de familles de spirales (spirales végétatives), l'une dans le sens des aiguilles d'une montre et l'autre dans le sens inverse, en quantités égales à deux nombres de Fibonacci consécutifs.
Les fleurs des Astaraceae en sont un exemple significatif : les graines du tournesol sont disposées selon deux groupes de spirales logarithmiques. Les éléments de l'inflorescence de la fleur se développent de manière à occuper le plus efficacement possible l'espace circulaire au centre de la fleur.
De la même manière que Bernoulli, nous pouvons conclure que l'émerveillement est le premier grand moteur de la recherche et de la passion pour la connaissance du monde qui nous entoure, et que les mathématiques ne sont qu'un outil de plus pour cultiver et approfondir cet émerveillement.



